Тема: Координаты вектора
Цели урока:
предметные – способствовать формированию умений нахождения координат вектора и рассмотреть правила действий над векторами с заданными координатами;
метапредметные – понимать и использовать математические средства наглядности для иллюстрации, интерпретации, аргументации; уметь самостоятельно планировать альтернативные пути достижения целей; выстраивать аргументацию, участвовать в диалоге, приводить примеры;
личностные – иметь целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
Задачи:
дать понятия: единичные координатные векторы, координаты вектора; разложение вектора по единичным векторам i и j
показать образцы оформления записей;
отработать полученные знания на примерах;
контроль знаний.
Тип урока: Комбинированный урок.
Вид урока: изучение нового материала (беседа) с последующим закреплением через решение задач.
Методы и приемы обучения: объяснительно-иллюстративный; частично-поисковый; словесный (фронтальная беседа); наглядный (демонстрация компьютерной презентации); практический.
Средства обучения: авторская презентация; учебник (Л.С.Атанасян, В.Ф.Бутузова, С.Б.Кадомцева и др. Геометрия. 7-9 классы. − М.: Просвещение, 2016) [2]
технические (компьютер, мультимедийный проектор).
План урока:
1.Организационный момент. (1 минута)
2. Повторение и закрепление пройденного материала. (4 минуты)
3. Изложение нового материала. (13 минут)
4. Физкультминутка. (3 минуты)
5. Закрепление изученного материала (10 минут)
6. Проверка усвоения новых знаний. (5 минут)
7. Подведение итогов. (2 минуты)
8. Рефлексия. (1 минута)
9. Домашнее задание. (1 минуты)
Х![]() ОД УРОКА
ОД УРОКА
I. Организационный момент.
1. Приветствие:
2. Организация рабочих мест:
Ребята, послушайте, какая тишина!
Это в школе начались уроки.
Мы не будем тратить время зря,
И приступим все к работе.
Мы сюда пришли учиться,
Не лениться, а трудиться.
Работаем старательно,
Слушаем внимательно.
— Проверьте ваши рабочие места: учебник, рабочая тетрадь, ручка.
I![]() I. Повторение и закрепление пройденного материала.
I. Повторение и закрепление пройденного материала.
1![]() . Проверка домашнего задания: № 911, 914 (б, в) (устно), решение задачи № 915 подготовить на доске.
. Проверка домашнего задания: № 911, 914 (б, в) (устно), решение задачи № 915 подготовить на доске.
2. Фронтальный опрос
1. Как называется теорема, доказывающая, что для любых двух коллинеарных векторов можно подобрать такое число, что один из векторов будет равен произведению второго вектора на это число?
2. Как записывается разложение двух коллинеарных векторов  ?
?
3.Чему равно число k, если вектора  сонаправлены ?
сонаправлены ?
4. Чему равно число k, если вектора  противоположно направлены ?
противоположно направлены ?
5. Можно ли разложить вектор по двум неколлинеарным векторам?
6![]() . Как записывается разложение вектора
. Как записывается разложение вектора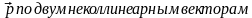
 ?
?
I![]() II. Изложение нового материала.
II. Изложение нового материала.
Повторим прямоугольную систему координат: оси координат, начало координат, единичный отрезок.
Р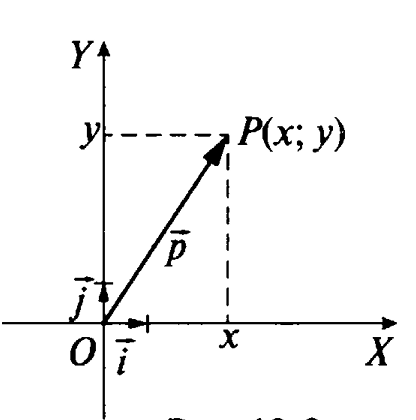 ассмотрим прямоугольную систему координат. Отложим от начала координат О единичные векторы (т.е. векторы, длины которых равны единице)
ассмотрим прямоугольную систему координат. Отложим от начала координат О единичные векторы (т.е. векторы, длины которых равны единице) 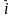 и
и  так, чтобы направление вектора
так, чтобы направление вектора 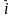 совпало с направлением оси Ох, а направление вектора
совпало с направлением оси Ох, а направление вектора  – с направлением оси Oy. Векторы
– с направлением оси Oy. Векторы 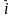 и
и  назовем координатными векторами.
назовем координатными векторами.
К оординатные векторы неколлинеарны, поэтому любой вектор р можно разложить по координатным векторам , т.е. представить в виде
оординатные векторы неколлинеарны, поэтому любой вектор р можно разложить по координатным векторам , т.е. представить в виде  = x
= x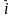 + y
+ y , причём коэффициенты разложения (числа x и y) определяются единственным образом. Коэффициенты разложения вектора
, причём коэффициенты разложения (числа x и y) определяются единственным образом. Коэффициенты разложения вектора  по координатным векторам называются координатами вектора
по координатным векторам называются координатами вектора  в данной системе координат. Координатные векторы будем записывать в фигурных скобках после обозначения вектора:
в данной системе координат. Координатные векторы будем записывать в фигурных скобках после обозначения вектора:  {х;у}.
{х;у}.
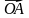 = 4
= 4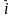 + 5
+ 5 ,
, 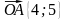
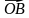 = — 6
= — 6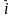 + 2
+ 2 ,
, 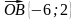
 = 5
= 5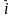 — 3
— 3 ,
, 
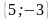
Нулевой вектор можно представить в виде
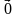 = 0 ·
= 0 · 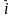 + 0 ·
+ 0 ·  ; его координаты равны нулю:
; его координаты равны нулю: 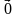 (0; 0).
(0; 0).
Координаты равных векторов соответственно равны.
Если  =
= 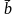 и
и  = x1
= x1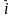 + y1
+ y1 ,
, 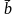 = x2
= x2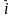 + y2
+ y2 , то х1 = х2, у1 = у2
, то х1 = х2, у1 = у2
Рассмотрим правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число (доказательства указанных правил учащиеся могут рассмотреть самостоятельно).
 (х1;у1) и
(х1;у1) и 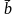 (х2;у2) – данные векторы
(х2;у2) – данные векторы
 =
=  +
+ 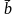 ;
; 
=
 –
– 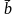 ;
;
![]() = k
= k , k – произвольное число
, k – произвольное число
I V. Физкультминутка.
— Не поворачивая головы, обведите взглядом стену класса по периметру по часовой стрелке, классную доску по периметру против часовой стрелки, треугольник, изображенный на стенде по часовой стрелке и равный ему треугольник против часовой стрелки. Поверните голову налево и посмотрите на линию горизонта, а теперь на кончик своего носа. Закройте глаза, сосчитайте до 5, откройте глаза и …
Мы ладонь к глазам приставим,
Ноги крепкие расставим.
Поворачиваясь вправо,
Оглядимся величаво.
И налево надо тоже
Поглядеть из под ладошек.
И – направо! И еще
Через левое плечо!
а теперь продолжим работу.
З акрепление изученного материала
1. Самостоятельно работают в тетради, один ученик за доской с последующей проверкой
Задача №1.
Выпишите координаты векторов
 = 2
= 2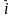 + 3
+ 3
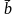 = —
= — + 2

 = 8
= 8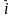 + 0
+ 0
=
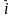 —
— 
= — 2
 =0
=0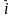 — 2
— 2
Задача № 2.
Запиши разложение по координатным векторам 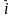 и
и  следующие вектора:
следующие вектора:
Задача №2.
Дано: векторы 
и
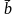
.
Найдите координаты векторов: а) =
 +
+ 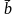 ; б)
; б) = 4
 ; в)
; в) = —
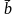 ;
;
г)  = 4
= 4 – 3
– 3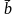 .
.
Решение.
Используя утверждения о координатах суммы векторов и произведения вектора на число, получаем:
а)
, тогда
б)
, тогда
в)
, тогда
г) обозначим через х1 и у1 абсциссу и ординату вектора  , через х2 и у2 — абсциссу и ординату вектора
, через х2 и у2 — абсциссу и ординату вектора 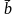 , буквами х и у — абсциссу и ординату вектора
, буквами х и у — абсциссу и ординату вектора  . Тогда х = 4х1 – 3 х2 = 4 · 2 – 3 · (-1) = 11; у = 4 у1 – 3 у2 = 4 · (-3) – 3 · 5 = — 27, тогда
. Тогда х = 4х1 – 3 х2 = 4 · 2 – 3 · (-1) = 11; у = 4 у1 – 3 у2 = 4 · (-3) – 3 · 5 = — 27, тогда 
.
О![]() твет: а)
твет: а)
; б)
; в)
; г)

.
П роверка усвоения новых знаний.
Самостоятельное решение задач. Учебник. [2]
Вариант I
Решить задачи № 912 (а, г); № 920 (г); № 988 (а, б); № 921 (а, в); № 914 (а).
Вариант II
Решить задачи № 912 (в, д); № 920 (д); № 988 (в, г); № 921 (б, г); № 914 (б).
![]()
Подведение итогов..
1. Какие векторы называются координатными?
2. Чему равны координаты вектора, если вектор можно разложить по координатным векторам?
3. Что вы можете сказать о координатах равных векторов?
4. Как найти координаты суммы двух векторов?
5. Как найти координаты разности векторов?
6. Как найти координаты произведения вектора на число?
Рефлексия
У вас на парте есть карточки настроения, выберите подходящую карточку и вклейте в тетрадь
Мне всё равно
Мне понравилось, я доволен собой
Мне грустно, я не всё усвоил
![]()
Домашнее задание.
1. П. 90, вопросы 7—8 (учебник, с. 244).
2. Решить задачи. № 918, 919, 926 (б, г) (учебник) [2]