Конспект урока по теме: Тетраэдр.Построение сечений

Урок по теме «Тетраэдр. Построение сечений». (слайд1)

(10 класс)

Цель:

образовательная

повторить понятие тетраэдра, изученные понятия, связанные со взаимным расположением прямых и плоскостей на примере тетраэдра;
научить изображать тетраэдр
организовать работу обучащихся по выработке умения строить сечения тетраэдра

развивающая

развивать пространственное мышление,
создать условия для развития познавательного интереса к предмету.

воспитательная

воспитывать интерес к математике,
воспитывать самостоятельность;
воспитывать правильное отношение к своему здоровью.

Оборудование:

ПК;
Мультимедийное оборудование;
Классная доска;
Учебники;
Тетради;
Школьные принадлежности;
Модели тетраэдра.

Тип урока: объяснение нового материала.

Формы работы: фронтальная, индивидуальная, самостоятельная, работа в парах

Методы контроля: устный

План урока

I Организационный момент

II .Мотивация. Постановка целей.

III Актуализация. Подготовка к изучению нового материала

IV Изучение нового материала

V Физ.минутка

V Закрепление учебного материала

VI Задание на дом

VII Рефлексия. Подведение итогов урока

Ход урока

Орг.момент.

Приветствие, проверка готовности к уроку.

Мотивация.

(слайд2)

— Что надо знать и уметь для решения данной задачи?

— Какова тема урока?

Постановка целей и задач урока.

Пространственное мышление- мысль, способная охватить Вселенную, включая ту её часть, для которой ещё не создано слов, сродни гениальности. (Аль Квотион) (слайд3)

Перед изучением нового материала учащимся предлагается вспомнить изученный материал о параллельных плоскостях, параллельности прямой и плоскости.

Активизация познавательной деятельности. Подготовка к восприятию нового материала.

Тест: (слайд 4)

Если две плоскости имеют общую точку, то

А) они называются скрещивающимися,

Б) они пересекаются по прямой, проходящей через эту точку,

В) они параллельны

2. Через прямую и не лежащую на ней точку

А) проходит плоскость и при том только одна

Б) проходит бесконечно много плоскостей

В) нельзя провести плоскость

3. Две прямые называются скрещивающимися, если

А) они лежат в одной плоскости и не пересекаются

Б) они не пересекаются

В) они лежат в одной плоскости и пересекаются

4. Если две точки прямой лежат в плоскости, то

А) прямая пересекает плоскость в некоторой точке

Б) прямая параллельна данной плоскости

В) все точки прямой лежат в данной плоскости

5. Если две прямые параллельны третьей, то

А) все три лежат в одной плоскости

Б) они параллельны

В) они скрещивающиеся

(Слайд 5). сверяем ответы. 1Б, 2А, 3Б, 4В, 5Б. (обосновываем ).

Изучение нового материала.

Одна из глав нашего курса будет посвящена многогранникам – поверхностям геометрических тел, составленным из многоугольников и их сечениям.

На прошлом уроке мы рассмотрели один из них, это тетраэдр. Вы подготовили сообщение о тетраэдре.

Сообщение. (Слайд 6) Рассмотрим произвольный треугольник АВС и точку Д, не лежащую в плоскости этого треугольника. Соединив точку Д отрезками с вершинами треугольника АВС, получим фигуру, которую назовём тетраэдром.

(слайд 7 ) Название этого многогранника пришло из Древней Греции, и в нём указывается число граней:

«тетра» — 4

«эдра» — грань

Тетраэдр является одним из правильных многогранников, которые мы рассмотрим на дальнейших наших уроках.

(слайд

Платоновыми телами являются:

Гексаэдр, Тетраэдр, Октаэдр, Икосаэдр, Додекаэдр.

(слайд 9) Платон считал, что мир строится из четырёх «стихий» — огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников, где Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у пламени.

(слайд 10) В жизни мы встречаемся с тетраэдром например в химии

Молекула метана СН4 имеет форму правильного тетраэдра. Этот факт подтверждается фотографиями молекулы метана, полученными при помощи электронного микроскопа.

Чтобы дать определение тетраэдра введём некоторые геометрические понятия.

У меня на столе имеются различные геометрические тела. Выберете среди них тетраэдр, будьте внимательны.

Выбрали все верно хотя у меня на столе была фигура очень похожая на тетраэдр, но имеет она в основании другой многоугольник, это пирамида.

Работа в тетрадях. Сейчас в тетради запишите число, тему «Тетраэдр и его сечения», и сделаем практическую работу.

Одну грань ABC называют основанием, а три другие – боковыми гранями.

Мы рассмотрим с вами построение сечения в тетраэдре

Что же такое сечение? (слайд 11)

Узнаем: какая плоскость называется секущей ?

Плоскость, по обе стороны которой имеются точки тетраэдра , называется секущей.

Узнаем: что называется сечением тетраэдра?

Секущая плоскость пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением.

Какими многоугольниками могут быть сечения? (слайд 12)

Так как тетраэдр имеет четыре грани, то его сечениями могут быть треугольники, четырёхугольники

Чтобы начать строить сечения мы должны с вами вспомнить некоторые геометрические утверждения

Работа у доски ( 1 ученик – на обороте, остальные в тетрадях) работа по чережу

1 В какой грани лежат т.М и N ?

2.Каково взаимное расположение (СD) и (AB) ?

3. Каково взаимное расположение (MN) и (ABC) ?

4.Какие грани пересекаются по (AD)?

5.Пересекаются ли (MК) и (АС) ?

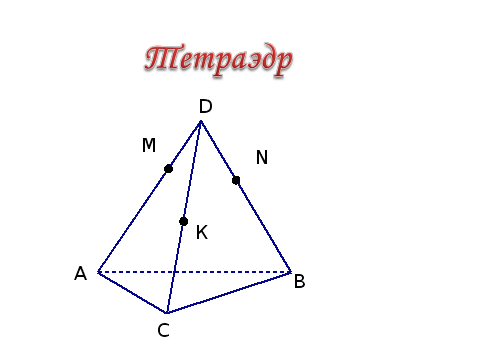
(слайд13)

ПАМЯТКА

Соединять можно только две точки, лежащие в плоскости одной грани.
Секущая плоскость пересекает параллельные грани по параллельным отрезкам.
Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.

Работа у доски ( 1 ученик – на обороте, остальные в тетрадях)

(слайды 27-33) Практическая работа: Построение сечения.

IV. Физ.минутка

Цель: восстановление работоспособности учащихся, воспитание правильного отношения к своему здоровью.

— А сейчас немного отдохнём.

В осенний период идёт распространение вируса ГРИППА, ОРВИ . Недаром в народе говорят, что инфекция распространяется с геометрической прогрессией. Есть много различных способов профилактики и лечения ОРЗ.

— Какие профилактические мероприятия вы проводите?

(Физ.рук проводит физ.минутку)

Работа с учебниками. СТР. 28 Рис 40 (а)

V. Закрепление учебного материала

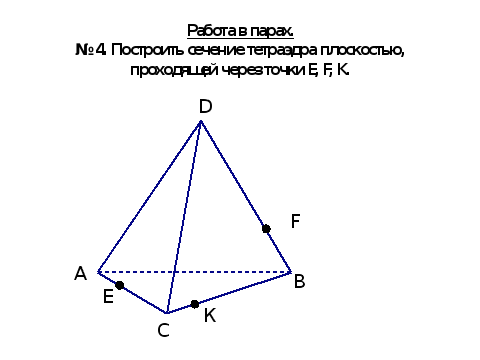
Работа в парах

№4. Построить сечение тетраэдра плоскостью, проходящей через точки E, F, K. ( 2 способа)

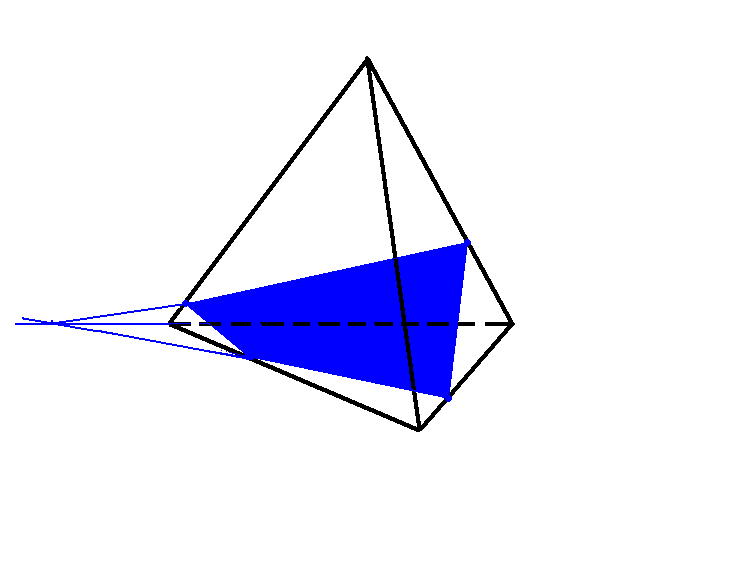
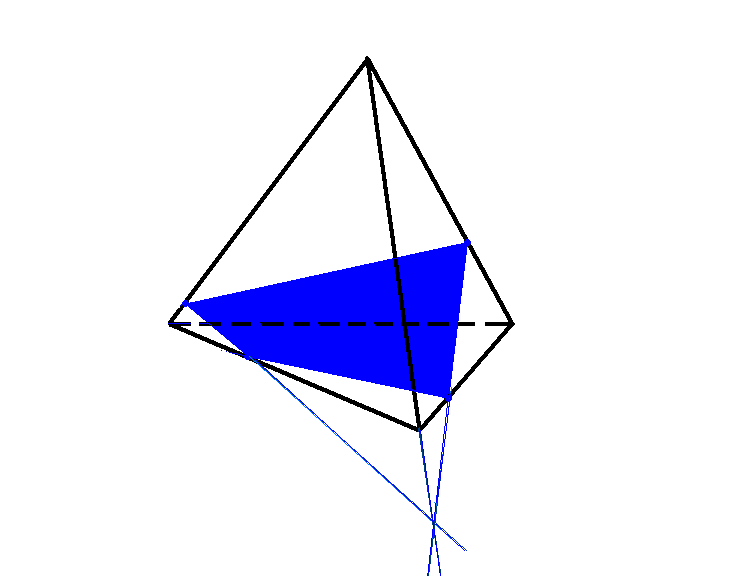
Устная работа

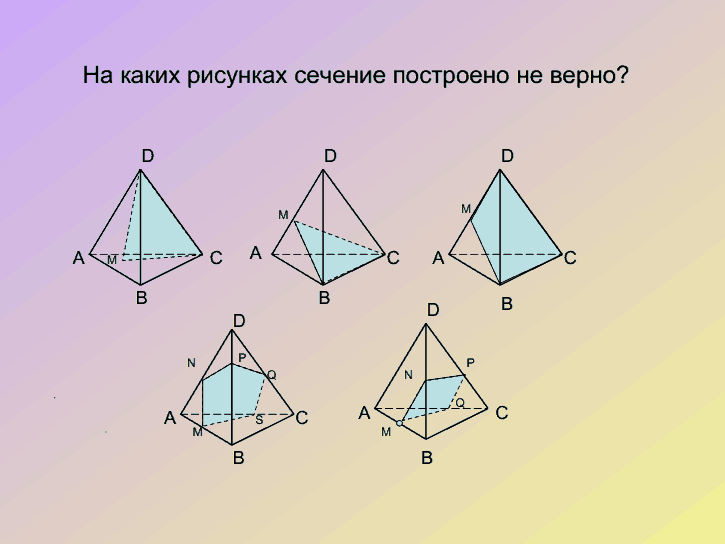
ИТОГ УРОКА:

О каком многограннике шла речь сегодня на уроке?
Какие задачи мы научились сегодня решать?
Какие действия должен уметь выполнять ученик для построения сечений многогранников? (находить точки пересечения прямой и плоскости; строить линию пересечения двух плоскостей)

ДОМАШНЕЕ ЗАДАНИЕ:

1) Стр 24-29

П.12, 14

2) Творческое задание (по желанию): изготовить бумажную модель тетраэдра.

3) № 75

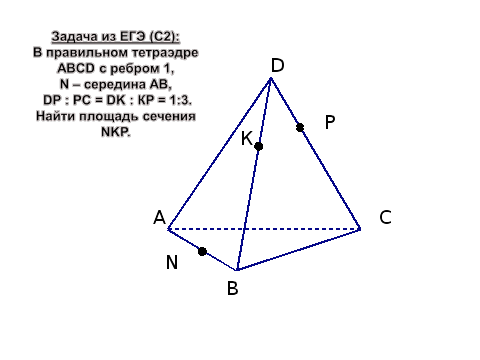
«4-5» Задача из ЕГЭ (С2):

В правильном тетраэдре АBCD с ребром 1,

N – середина AB,

DP : PC = DK : КВ = 1:3.

Найти площадь сечения NKP.

VII Рефлексия. Подведение итогов урока

Цель: подведение итогов урока, развитие у учащихся навыков самоконтроля.

Задача учителя: дать оценку успешности достижения цели и наметить перспективу на будущее.

— Что нового мы узнали на уроке?

Мне хочется вернуться к нашему девизу «Прогрессио – движение вперёд!

Учащимся предлагается поставить на значок + на линии в том месте, которое отражает их отношение к занятию и степень участия в уроке:

1. Я считаю, что занятие было интересным___________________скучным.

2.Я научился многому ______________________малому.

3. Я думаю, что слушал других внимательно__________________невнимательно.

4. Я принимал участие в дискуссии часто________________________редко.

5. Результатами своей работы на уроке я доволен_________________не доволен.

-Как вы думаете, а мы сегодня добились прогресса?

-В чём заключается наш прогресс?

(Оценки за урок)

Всего вам хорошего! Спасибо за урок!

Самоанализ урока.

Урок «Тетраэдр и его сечения» завершает изучение темы «Параллельность прямой и плоскости», которая является первой при изучении темы стереометрии – раздела геометрии. Одной из основных задач геометрии является формирование пространственного представления, и данный урок позволяет выполнить эту задачу.

На уроке спланировано включение учащихся в осознанную деятельность.

Избранные методы: информационные (объяснение с демонстрацией наглядных пособий) и репродуктивные (беседа с элементами самостоятельной работы) и формы организации познавательной деятельности были нацелены на достижение триединой цели урока.

Задачей на уроке было организовать деятельность учащихся таким образом, чтобы подвести их к теме урока, расширить знания о тетраэдре, научить строить сечения.

На первом этапе урока, используя проблемный вопрос, определили темы урока и целей.

На этапе (изучение нового материала) показать возможные сечения тетраэдра, научиться строить разные сечения.

Этап закрепления предполагал возможность учащихся самостоятельно построить различные сечения параллелепипеда.

ИТОГ урока.

В конце урока проведена рефлексия, которая побуждала учащихся к самоанализу и оценке деятельности.

Домашнее задание позволит учащимся поработать с учебником.

Приложения.

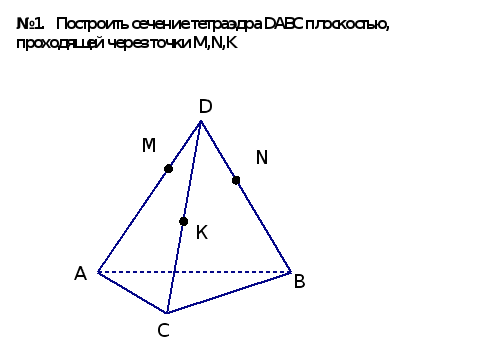
№1. Построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K

Построение.

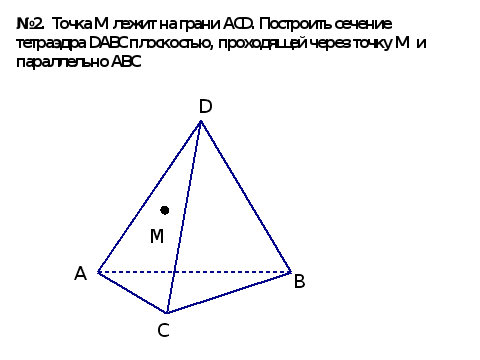
№2. Точка М лежит на грани ACD. Построить сечение тетраэдра DABC плоскостью, проходящей через точку M и параллельно АВС

Построение.

№ 3. Построить сечение тетраэдра плоскостью, проходящей через точки E, F, K.

Построение.

№ 4. На ребрах AC, AD, DB тетраэдра – DABC. Отмечены точки M,N,P. Построить сечение тетраэдра плоскостью MNP.

1способ. Построение. 2 способ. Построение.