Разработка урока по теме "Пирамида"

Суходольский горный колледж

РАЗРАБОТКА УРОКА ПО ГЕОМЕТРИИ

НА ТЕМУ:

Тема. «Пирамида. Правильная пирамида».

Цели урока:

Учебная — сформировать понятие пирамиды и ее основных элементов;
дать понятие правильной пирамиды и ее свойства.
Развивающая – формирование познавательной активности и самостоятельности при изучении материала;
Развитие мировоззрения учащихся.
Воспитательная – привитие культуры учебного процесса.

Тип урока: урок усвоения новых знаний

Оборудование: модели пирамид; плакаты; компьютеры; видеофрагменты

Содержание:

Вступление

Историческая точка зрения
Происхождение слова «пирамида»
Математическая точка зрения

Изучение нового материала

Определение пирамиды
Виды пирамид
Правильная пирамида
Свойства правильной пирамиды
Площадь поверхности пирамиды

Закрепление изученного
Пирамиды во Вселенной

Стоит на земле пирамида,

И боги о ней говорят.

На ней не рванье, не хламида,

А вечного камня наряд.

Она здесь стоять не устала,

Хоть минуло много веков,

Она головою достала

До самых седых облаков

Что людям она сохранила?

Великих камней забытье?

Зрачки желтоглазого Нила

Лениво глядят на нее.

Кто спит в этой древней могиле?

Расскажут ли камни о том,

Как всех их слезами солили

И кровью кропили потом.

Стоит на Земле пирамида,

И боги о ней говорят.

На ней не рванье, не хламида,

А вечного камня наряд.

(С. Островой)

1. Вступление

Историческая точка зрения

ПИРАМИДА, монументальное сооружение, имеющее геометрическую форму пирамиды (иногда ступенчатую или башнеобразную). Пирамидами называют гробницы древнеегипетских фараонов
3 – 2-го тыс. до н. э., а также постаменты храмов в Центральной и Южной Америке, связанные с космологическими культами.

Терра-Лексикон: Иллюстрированный

энциклопедический словарь, 1998

Происхождение слова «пирамида»

Слово «пирамида», возможно, произошло от названия формы хлебцов в Древней Греции (piros – рожь) или от египетского выражения (per me ous – боковое ребро сооружения). Еще одно толкование – «пирамида» происходит от «пирамис» этимологически связано с «пир» – «огонь»; обозначая символическое представление Единого Божества пламени, жизни всех созданий.

Посвященные прошлого считали пирамиду идеальным символом Тайной Доктрины – символом иерархии, существующей во вселенной.

Математическая точка зрения

Евклид пирамиду определяет как телесную фигуру, ограниченную плоскостями, которые от одной плоскости сходятся к одной точке.

Герон предложил следующее определение пирамиды: «Это фигура, ограниченная треугольниками, сходящимися в одной точке и основанием которой служит многоугольник».

2. Изучение нового материала

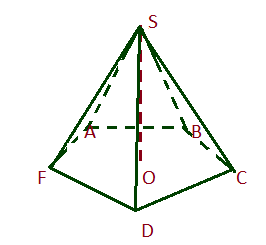
Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, — вершины пирамиды и всех отрезков, соединяющих вершину с точками основания.

Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.

Поверхность пирамиды состоит из основания и боковых граней. Каждая грань пирамиды – треугольник.

Высота пирамиды – перпендикуляр, опущенный из вершины на плоскость основания.

Высота проецируется в вершину основания (SA)

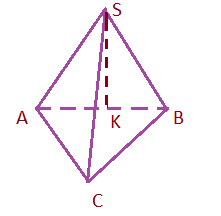
Высота проецируется на сторону основания (SK)

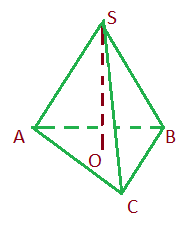
Высота проецируется во внутреннюю область основания (SO)

Высота проецируется во внешнюю область основания (SK)

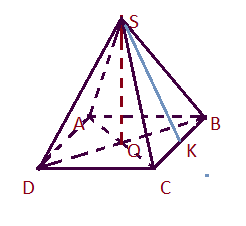
Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника.

Осью правильной пирамиды называется прямая, содержащая ее высоту.

Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой (SK).

Свойства правильной пирамиды

SA=SB=SC=SD
Боковые ребра образуют равные углы с плоскостью основания
Боковые ребра образуют равные углы с высотой
Боковые грани образуют равные углы с основанием
Высота пирамиды образует равные углы с высотами боковых граней

Боковой поверхностью пирамиды называется сумма площадей ее боковых граней.

Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.

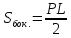
Полная поверхность пирамиды равна сумме площадей боковой поверхности и основания.

3. Закрепление изученного

Ответьте на вопросы:

1. Как называется треугольная пирамида?

2. Как называются прямые, соединяющие вершину пирамиды с вершинами основания?

3. Какие два условия должны быть выполнены, чтобы пирамида была правильной?

4. Сколько граней, перпендикулярных к плоскости основания, может иметь пирамида?

5. Существует ли четырехугольная пирамида, у которой противоположные боковые грани перпендикулярны к основанию?

6. Всегда ли высота пирамиды проецируется в центр основания?

7. Что называется апофемой?

8. Из чего состоит поверхность пирамиды?

9. Как вычислить боковую поверхность правильной пирамиды?

10. Может ли правильная пирамида быть шестиугольной?

Заполните таблицу:

Дана правильная четырехугольная пирамида.

а – сторона основания; L – апофема; S_бок. – боковая поверхность пирамиды; S_осн. – площадь основания; S_полн. – площадь полной поверхности пирамиды; р – периметр основания.