Применение элементов технологии УДЕ при изучении рациональных чисел в 6 классе.

Применение элементов технологии УДЕ при изучении рациональных чисел в 6 классе.

Новое направление в теории и практике математического образования, предлагаемое академиком П. М.Эрдниевым, комплексно использует открытия всех наук о мышлении для решения насущных задач обучения и воспитания.

Укрупненная дидактическая единица (УДЕ) обладает качествами системности и целостности, устойчивостью к сохранению во времени и быстрым проявлением в памяти. Это понятие вобрало воедино следующие конкретные методы обучения:

Совместное и одновременное изучение взаимосвязанных действий и операций, функций, теорем ( в частности, взаимообратных);
Обеспечение единства процессов решения и составления задач( уравнений, неравенств и т.д.);
Рассмотрение во взаимопереходах определенных и неопределенных знаний ( в частности деформированных упражнений);
Обращение структуры упражнения, что создает условия для метода противопоставления исходного и преобразованного заданий;
Выявление сложной природы математического знания;
Реализация принципа дополнительности в системе упражнений ( понимание достигается в результате межкодовых переходов между образным и логическим компонентами мышления).

При укрупнении дидактических единиц рационально используются «скрытые» (подсознательные) резервы мышления, существенно повышается результативность обучения в целом.

Эффективность и доступность методики УДЕ доказана практически и объяснима научно:

— она основана на систематическом противопоставлении парных суждений ( И.П. Павлов) и структурировании в мышлении циклических связей ( П.К. Анохин);

— в структуре УДЕ обеспечивается теснейшая связь левополушарного и правополушарного мышления, являющегося крупнейшим открытием нейрофизиологии.

Усвоение материала осуществляется в процессе выполнения упражнений, а потом и развитие методики идет по пути внедрения новых форм и видов математических упражнений, вызывающих у школьников большую мыслительную активность. Опыт обучения на основе УДЕ показал, что основной формой упражнения должно стать составное задание, образующиеся из нескольких логически разнородных, но психологически состыкованных в некоторую целостность частей. Например:

а). решение обычной задачи;

б). составление обычной задачи и ее решение;

в). составление задачи по некоторым элементам общим с исходной задачей (аналогичной);

д). решение или составление задачи, обобщенной по тем или иным параметрам исходной задачи.

Главное в работе над укрупненными упражнениями в том, чтобы все составные части по возможности были выполнены в указанной последовательности на одном занятии( при нехватке времени выполнялись хотя бы устно и обсуждались кратко, в крайнем случае завершались бы в домашней работе).

Использование элементов УДЕ на уроках математики экономит 20% учебного времени, что позволяет:

— уделить больше внимания решению задач;

— ознакомить учащихся с основными базовыми понятиями геометрии, с типами и особенностями оформления геометрических задач;

— подготовить базу для изучения полного школьного курса геометрии 7-11 кл.;

— изложение материала крупными блоками способствует усвоению главных понятий, увеличению объема знаний при значительном сокращении нагрузки на ученика.

Изучение отрицательных чисел остается одним из самых сложных вопросов программы 6-7 классов. Тому есть несколько причин. Во- первых, традиционно отрицательные числа изучаются после обыкновенных и десятичных дробей ( учебник Н. Я. Виленкина). При таком порядке изучения, усвоения правил нахождения знака результата, осложняется наличием различных алгоритмов выполнения действий с модулями. Во-вторых, в отличие от натуральных чисел и дробей, изучение отрицательных чисел не опирается на предшествующий опыт предметной деятельности, подводящий учащихся к пониманию правил действия с этими числами.

Использование элементов технологии УДЕ позволяет лучше усваивать учащимися действия с отрицательными числами. На разных этапах изучения этой темы можно использовать всевозможные задания, так называемые многокомпанентные и дифференцированные.

Рациональные числа ( введение понятия рационального числа, положительного и отрицательного числа).

Числа, которым соответствуют точки, лежащие на координатной прямой 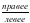начала координат, называют.

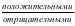Сказанное о рациональных числах как о значениях величин, которые могут изменяться в двух противоположных смыслах, удобно представить в виде таблицы:

Отрицательным числом выражается	Числом нуль выражается	Положительным числом выражается
Координата точки, лежащей на оси координат левее точки О( начала координат)	Координата точки О- начала координат.	Координата точки, лежащей на оси координат правее точки О( начала координат
Расход ( денег, воды, топлива и т. д.)		Приход ( денег, воды, топлива и т. д.)
Убыток ( в руб)		Прибыль ( в руб).
Температура ниже нуля градусов( точки замерзания воды или точки таяния льда)	Температура таяния льда ( замерзания воды)	Температура выше нуля градусов( точки замерзания воды или точки таяния льда
Глубина ниже уровня океана ( в м. или км).	Уровень океана	Высота выше уровня океана ( в м.или км).
Время до нашей эры ( в годах, веках)	Начало христианского летосчисления ( начало нашей эры).	Время нашей эры ( в годах, веках)

Предлагаются следующие задачи:

а). Изобразить на координатной прямой результат следующих перемещений: сначала из т. О тело переместилось на 5 ед. вправо, а потом еще на 2 ед. влево. Тело оказалось в т. С. Назвать координату т.С.

б).Решить предыдущую задачу, поменять всюду слово « вправо» на слово «влево». Назвать координату точки Д, в которой оказалось тело при перемещении влево.

в). Записать в таблицу пропущенные высказывания:

С помощью рациональных чисел ( со знаком «+» или «-«

Без использования знака числа

-250
Температура утром была -6°С
…
…
Уровень Каспийского моря – 28 м от уровня океана
…

Уровень воды в реке во время паводка составляет 120 см от ординара (нормального уровня)
Уровень воды в реке см…

Убыток в хозяйстве составил 250 р.
° мороза
Термометр показывал 15°С мороза.
Температура тела человека 37°С.
На м ниже…

Данная точка местности находится на высоте 250м над уровнем океана.
… выше ординара на…

Уровень воды в реке упал ниже ординара на 80 см.

II. Сравнение рациональных чисел.

_{Из двух рациональных чисел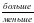} то, которое расположено на координатной оси _.

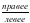_{Предлагаются задания:}

_{1)по рисунку установить взаимное положение точек и сравнить их координаты. (Записать словами и с помощью знаков).}

_{Образец.}

_{Точка А левее точки С; -4}

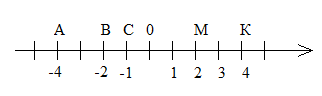
а) В левее , значит

б) К правее ,

в) т. О правее т. В,

г) С левее К,

д) правее , .

2) а) Написать вместо клеток числа в следующих сравнениях, нарисовать соответствующие точки на оси координат.

б) Проверить ряд неравенств : -300

в) Расположить в порядке возрастания следующие рациональные числа: -0,03; 10; -10; 4; 1,0001; -3; 0; -40000.

г) Расположите в порядке убывания следующие числа: -1,001; 2,3; 4000; -3000; -2,3; 6,2; -0,0002; 0,0001.

3) а) Подобрать два отрицательных числа, такие, чтобы выполнялись два соотношения:

| |

б) Подобрать два положительных числа, таких, чтобы выполнялись два соотношения:

| | | |.

III. Сложение и вычитание рациональных чисел.

Чтобы найти сумму двух рациональных чисел одинакового знака, надо сложить их модули и перед суммой модулей записать общий знак данных чисел.

(+5) + (+2) = +7

(-5) + (-2) = -7

(±5)+(±2) = ±7.

Выполнить действия над рациональными числами:

а) 6 + 3 = б) 4 + = 7

-6 + (-3) = -4 + = -7

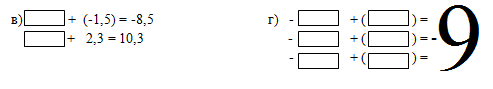
Чтобы найти сумму двух рациональных чисел разных знаков, надо их большего модуля вычесть меньший и перед разностью модулей написать знак того числа, модуль которого больше.

Выполнить сложение:

а) 7 + 3 = б) 4 + (-6) = в) 8 + (-5) =

7 + (-3) = 4 + 6 = — 8 + 5 =

— 7 + 3 = -4 + (-6) = 2 + (-6) =

— 7 + (-3) = — 4 + 6 = — 2 + 6 =

3) Записать пропущенные числа в равенствах:

+ 5 = 9 + 5 = 6

+ (-5) = -9 + 7 = 6

+ 3 = — 8 + (-3) = 0

+ (-3) = -8 (-6,5) + = 0.

Чтобы вычесть рациональное число, достаточно прибавить противоположное число

а –b = a + (-b)

3)Выполнить вычитание и проверить ответ сложением:

а) 5 – (-3) = б) – 3 – (-10) =

5 – 4 = — 3 – (-12) =

— 7 – (-2) = 2 – (-1) =

— 8 – 6 = 2 – (-9) =

Выполнить сложение и проверить ответ вычитанием:

а) — 6 + (-3) = б) –10 + 20 =

— 6 + 4 = — 9 + 19 =

— 4 + 10 = 7 + (-12) =

— 4 + (-8) = — 7 + 13 =

4)Решить уравнение и проверить найденный корень:

1)х + (-6) = 10; 2) у – 7 = — 20;

-8,5 + а = 12,5; 15,8 – b = -4,2;

3) х + 9 = -13; 4) у – (-3) = -10;

-10,2 + а = 3,1; 25,7 – b = -13,6.

5) Сравнить два числа и поставить между ними вместо знак сравнения:

а) – 6 – (-6) в) 7 -7

б) – 6 – 6 г) 7 – (-7)

III. Умножение и деление рациональных чисел.

Произведение двух чисел знаков есть число .

(+ ) · (+ ) = (+ );

(- ) · (- ) = (+ );

(+ ) · (- ) = (- );

(- ) · (+ ) = (- ).

Вычислить:

а) – 6 · ( — 21) · 1 · (- 3);

б) 1 · ( — · (- 5) · 2 · (- 3) · 2 · (- 1).

Подобрать несколько сомножителей для данного произведения:

а) · = — 12; в) · · (- 6) = — 30;

б) · · (- 6) = 24; г) · (- 10) · 2 = 40.

Чтобы разделить одно число на другое, надо модуль делимого разделить на модуль делителя и перед этим частным поставить знак , если делимое и делитель имеют знаки.

Записать пропущенные числа:

а) 25: (-2) = -12,5; б) : (-1) = 7;

-40 : 8 = ; 12 : = -6;

40 : (-8) = ; · 2 = -24;

25 : (-8) = ; — 4 · = 20.

в) Выполнить действие и проверить обратным действием:

(-20) : (-0,5);

42: (-7); : .

г) Решить уравнение и проверить корень:

х : (-3,5) = -3; х · (-0,14) = -2,2;

-6 · х = 16; -100 : х = -0,5.

Решить четверку примеров, составленных из данных чисел на действия первой ступени; проверить ответы вычислением:

Образец:

2; 5; 7.

2 + 5 = 7; 7 – 5 = 2;

5 + 2 = 7; 7 – 2 = 5.

-12; -8; -20.

— 12 + (-8) = — 20;

— 20 – (-8) = ;

+ = — 20;

— = .

Решить четверки примеров, составленных из данных чисел на действия второй ступени:

а) 2; -5; -10.

— 2· (-5) = — 5 · 2 =

-10: (-5) = : =

б) -12; -8; 96.

-12· (-8) = ; -8 · (-12) = ;

96: (-8) = ; : = .